BabbleDay's Blog

LeetCode Plus One

心得：想清楚，打草稿，避免不必要的错误

记录是否进位

class Solution:
    # @param {integer[]} digits
    # @return {integer[]}
    
    def plusOne(self, digits):
        i, carry = -1, True
        while(carry):
            if digits[i]==9:
                digits[i] = 0
                if i==-len(digits):
                    digits = [1] + digits
                    carry = False
                i -= 1
            else:
                digits[i] += 1
                carry = False
        return digits

是九变0，最高位加［1］

class Solution:
    # @param {integer[]} digits
    # @return {integer[]}
    def plusOne(self, digits):
        i = -1
        while(not i<-len(digits)):
            if digits[i] != 9:
                digits[i] += 1
                return digits
            else:
                digits[i] = 0
            i -= 1
        digits = [1] + digits
        return digits

LeetCode Remove Duplicates from Sorted Array

使用del删除list里的元素

class Solution:
    # @param {integer[]} nums
    # @return {integer}
    def removeDuplicates(self, nums):
        i, j = 0, 1
        if len(nums)<2:
            return len(nums)
        while(i < len(nums)-1):
            j = i+1
            if nums[i] == nums[j]:
                del nums[j]
            else:
                i += 1
        return len(nums)

不改变list

class Solution:
    # @param {integer[]} nums
    # @return {integer}
    def removeDuplicates(self, nums):
        l, i = 1, 1
        if len(nums)<2:
            return len(nums)
        for i in range(1,len(nums)):
            if nums[i]!=nums[i-1]:
                nums[l] = nums[i]
                l += 1
        return l

Leetcode Remove Element

利用Python的list comprehension想写出一行代码

class Solution:
    # @param {integer[]} nums
    # @param {integer} val
    # @return {integer}
    
    def removeElement(self, nums, val):
        # nums = [x for x in nums if x!=val]
        z = [y for y in nums if y != val]
        for k,v in enumerate(z):
            nums[k] = v
        return len(z)

但是题目要求要在原地修改list的内容，所以原来就想着直接给nums赋值，结果大错特错！

问题在于，Python中的Naming是将一个名字和一个Object绑定即binding，而不是以前的assign。带图的解释戳这里

而且Python的binding是有作用域的，即scope。在一个作用域里的绑定是不会在子作用域里被改变的。

在这里就是，大环境下绑定了nums(原），而在函数中重新建立了一个list并用nums（新）去绑定了。当函数执行完毕之后，回到大环境下，nums其实还是nums（原），所以之前的写法会错。

这一段论述可以由下图验证：

那这样的解决办法就是在函数中，给nums（原）绑定的对重写。即for k,v in enumerate(z): nums[k] = v。

LeetCode Majority Element

利用此题中众数次数超过一半的特性 O(n)

class Solution:
    # @param {integer[]} nums
    # @return {integer}
    def majorityElement(self, nums):
        count, temp = 1, nums[0]
        for x in nums[1:]:
            if x==temp:
                count += 1
            else:
                count -= 1
            if count==0:
                temp = x
                count = 1
        return temp

哈希表 O(n)

LeetCode Contains Duplicate

位操作 O(n)

class Solution:
    # @param {integer[]} nums
    # @return {boolean}
    def containsDuplicate(self, nums):
        pos, neg = 0, 0
        for x in nums:
            if x < 0:
                temp = 1 << -x
                if neg & temp != 0:
                    return True
                pos |= temp
            else:
                temp = 1 << x
                if pos & temp != 0:
                    return True
                pos |= temp
        return False

哈希表 O(n)

Python一行

Recursion

ComposingPrograms 1.7 Exercises

def countdown(n):
    print(n)
    if n>1:
        countdown(n-1)

def countup(n):
    if n>0:
        countup(n-1)
        print(n)

def recursive(m,n):
    if n>0:
        return m + recursive(m, n-1)
    else:
        return 0

def expt(base, power):
    if power==0:
        return 1
    else:
        return base * expt(base, power-1)

def sum_digits(n):
    if n<10:
        return n
    else:
        return n%10 + sum_digits(n//10)

def is_prime(n, d):
    if n<=1:
        return False
    elif d==1:
        return True
    elif n%d==0:
        return False
    else:
        return is_prime(n, d-1)

def sum_primes_up_to(n):
    if n==2:
        return 2
    elif is_prime(n, n-1):
        return sum_primes_up_to(n-1) + n
    else:
        return sum_primes_up_to(n-1)

递归和信用卡的Luhn算法

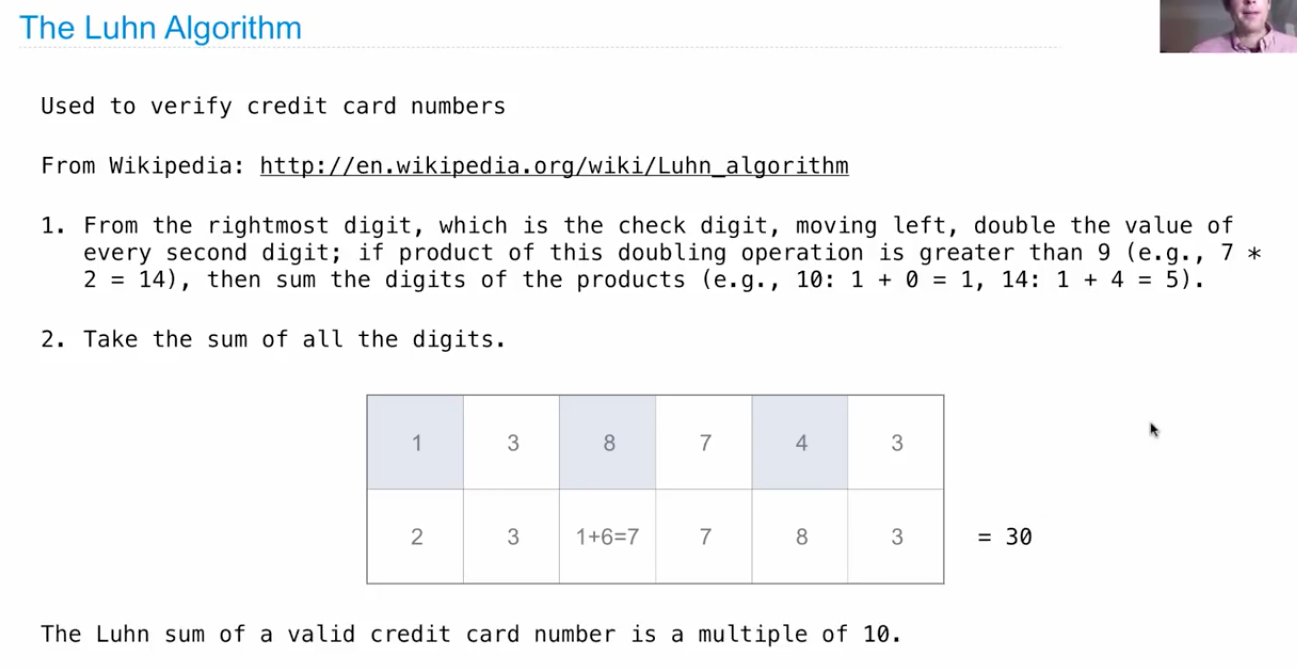
这里用python做一个mutual recursion

def split(n):
    return n//10, n%10

def luhn_sum(n):
    if n<10:
        return n
    else:
        rest, last = split(n)
        return luhn_double_sum(rest) + last

def luhn_double_sum(n):
    rest, last = split(n)
    luhn_digit = split(2*last)[0] + split(2*last)[1]
    if n<10:
        return luhn_digit
    else:
        rest, last = split(n)
        return luhn_sum(rest) + luhn_digit

Newton's Method

寻找函数零点：Quickly finds accurate approximations to zeros of differenciable functions.

只要问题是可微的，则问题是可解的。

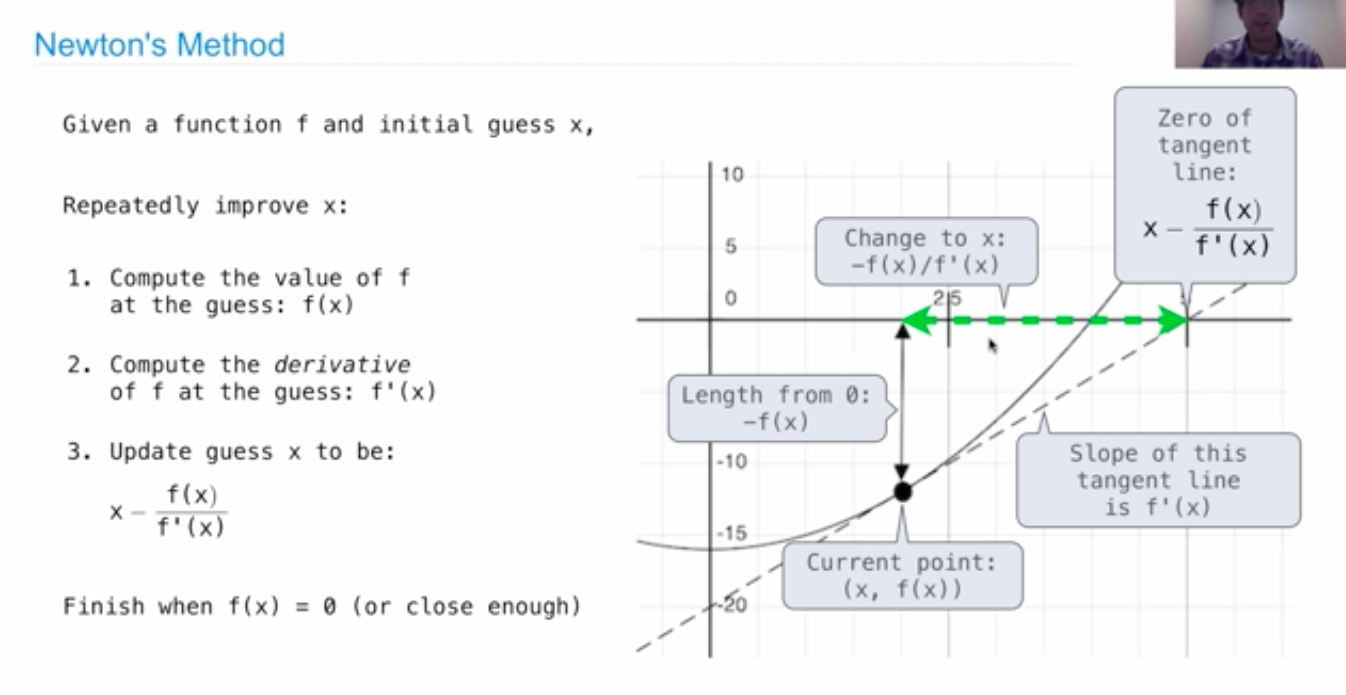
Wikipedia上操作演示

https://en.wikipedia.org/wiki/Newton's_method#/media/File:NewtonIteration_Ani.gif

实现指南：

高阶函数为的是抽象出功能，不要被参数混乱思路

python中整数相除会返回整数，所以注意传入浮点数做参数

def square_root(a):
    def f(x):
        return x * x - a

    def df(x):
        return 2 * x

    return find_zero(f, df)

def find_zero(f, df):
    def near_zero(x):
        return appro_equal(f(x), 0)
    return improve(update(f, df), near_zero, guess=1.0, max_update=100)

def update(f, df):
    def u(x):
        return x - f(x)/df(x)
    return u

def improve(update, close, guess, max_update):
    k = 0
    while not close(guess) and k < max_update:
        print guess, k
        guess = update(guess)
        k += 1
    return guess  # the guess improved

def appro_equal(x, y, tolerance=1e-15):
    print abs(x-y) < tolerance
    return abs(x-y) < tolerance

推广至求n次根

>>> def power(x, n):
        """Return x * x * x * ... * x for x repeated n times."""
        product, k = 1, 0
        while k < n:
            product, k = product * x, k + 1
        return product
>>> def nth_root_of_a(n, a):
        def f(x):
            return power(x, n) - a
        def df(x):
            return n * power(x, n-1)
        return find_zero(f, df)

实际应用 Function Decorator

def trace(fn):
    def t(x):
        print "Calling", fn, "on argument", x
        return fn(x)
    return t

@trace
def square(x):
    return x * x

Higher-Order Functions in Python

学习资料：

http://composingprograms.com/pages/16-higher-order-functions.html

定义：

Higher-Order functions can accept other functions as arguments or return functions as values.

例一：计算黄金比例

def improve(update, close, guess=1):
    while not close(guess):
        guess = update(guess)
    return guess

def golden_update(guess):
    return 1/guess + 1

def square_close_to_successor(guess):
    return approx_eq(guess * guess,
                     guess + 1)

def approx_eq(x, y, tolerance=1e-3):
    return abs(x - y) < tolerance

phi = improve(golden_update,
              square_close_to_successor)

Two key advantages of lexical scoping in Python.

函数命名只与定义环境有关，与执行环境无关
The names of a local function do not interfere with names external to the function in which it is defined, because the local function name will be bound in the current local environment in which it was defined, rather than the global environment.
执行函数由内向外延展
A local function can access the environment of the enclosing function, because the body of the local function is evaluated in an environment that extends the evaluation environment in which it was defined.

例二：

def average(x, y):
    return (x + y)/2

def improve(update, close, guess=1):
    while not close(guess):
        guess = update(guess)
    return guess

def approx_eq(x, y, tolerance=1e-3):
    return abs(x - y) < tolerance

def sqrt(a):
    def sqrt_update(x):
        return average(x, a/x)
    def sqrt_close(x):
        return approx_eq(x * x, a)
    return improve(sqrt_update, sqrt_close)

result = sqrt(256)

函数计算时层层隔离，名字重复无影响。但是对于大工程来说，明明冲突可能给自己带来麻烦，比如需要重命名的时候。

def square(x):
    return x * x

def successor(x):
    return x + 1

def compose1(f, g):
    def h(x):
        return f(g(x))
    return h

def f(x):
    """Never called."""
    return -x

square_successor = compose1(square, successor)
result = square_successor(12)