BabbleDay's Blog
Happy Coding
【计算几何】基本概念与实现
向量的运算,点到直线的距离,多边形面积,线线相交,已知不共线三点XYZ求其圆心和半径,求已知点X关于已知直线Ax+By=C的对称点,关于某点的旋转
-
二维向量的点乘:A ⋅ B = |A||B|Cos(θ) <=> (x1, y1).(x2, y2) = x1*x2 + y1*y2
垂直点积为零,平行点积最大 -
二维向量的叉乘:A x B = |A||B|Sin(θ) <=> (x1, y1)x(x2, y2) = x1*y2 - y1*x2
逆时针为正,顺时针为负——其实是由坐标系决定的
向量积的绝对值是其对应平行四边形的面积,红线是面积的一半 - 点到直线的距离(已知直线上两点):(AB AC)/|AB| 注意因为AB x AC是矢量有正负,最后要取绝对值
-
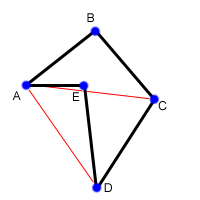
多边形面积:S = abs( AB x AC + AC x AD + AD x AE ) / 2
按顺序来,向量积正负自动抵消~ 注意最后除以2,可能要double
-
int area = 0; int N = lengthof(p); //We will triangulate the polygon //into triangles with points p[0],p[i],p[i+1] for(int i = 1; i+1<N; i++){ int x1 = p[i][0] - p[0][0]; int y1 = p[i][1] - p[0][1]; int x2 = p[i+1][0] - p[0][0]; int y2 = p[i+1][1] - p[0][1]; int cross = x1*y2 - x2*y1; area += cross; } return abs(cross/2.0);



-
-
线线相交:理想的直线方程 Ax+By=C ——(A,B)是直线的法向量
若已知直线两点(x1, y1) and (x2, y2),则A = y2-y1 B = x1-x2 C = A*x1+B*y1
从而有
A1x + B1y = C1
A2x + B2y = C2
两直线平行 <=> 两直线法向量平行 <=> (A1,B1)x(A2,B2)= 0 // 然后求交点就是中学的公式了
如果是两条线段从(x1,y1) 到 (x2,y2)而不是直线,注意检验所求交点在不在线段上:
分别对两条线段检查,注意考虑浮点数的精确度的影响
min(x1,x2) ≤ x ≤ max(x1,x2) 和 min(y1,y2) ≤ y ≤ max(y1,y2)double det = A1*B2 - A2*B1 if(det == 0){ //Lines are parallel }else{ //Get the intersection double x = (B2*C1 - B1*C2)/det double y = (A1*C2 - A2*C1)/det } -
已知不共线三点XYZ求其圆心和半径
S1 直线XY和YZ:Ax+By=C A=Yy-Xy B=Xx-Xy
S2 直线的垂线:-Bx+Ay=D
S3 带入中点求得D
S4 两直线交点得圆心 -
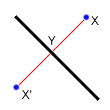
求已知点X关于已知直线Ax+By=C的对称点
S1 对称点连线的直线 -Bx+Ay=D
S2 带入X得到D
S3 两直线交点Y
S4 X-Y=Y-X' => X'=2Y-X -
关于某点的旋转 <=> 旋转点绕原点旋转后平移至某点
将点(x,y)绕原点逆时针旋转θ度
x' = x Cos(θ) - y Sin(θ) and y' = x Sin(θ) + y Cos(θ)
/* cos example */#include <stdio.h> /* printf */ #include <math.h> /* cos */ #define PI 3.14159265 int main () { double param, result; param = 60.0; result = cos ( param * PI / 180.0 ); printf ("The cosine of %f degrees is %f.\n", param, result ); return 0; }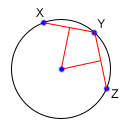
2022年9月29日 22:31
In modern days, Computer Education is most important for everyone and its one of the fastest growing career fields. A career in the field of computer science has been proven to be a worthwhile direction for any young enthusiast. It helps them to aim for excellent jobs in the future and succeed in it. NCERT Computer Sample Paper Class 9 The computer has become a standard of education throughout the world. This makes computer education important.In modern days, Computer Education is most important for everyone and its one of the fastest growing career fields.